The purpose of this post is to explore and discover the number of permutations of a childrens 16 piece train track set.
The trainset of interest is the following:

This particular trainset has a total of 16 track piecies, 12 curved and 4 straight. The curved pieces are reversible (the straight ones are not) and 2 of the 4 straight pieces form a bridge as in the picture. I am interested in all solutions, for example those that use 10 or 12 pieces, not just all 16. Additionally, I want to solve this programatically and to create a visual representation of the solutions. A solution will be presented that uses Python to solve it programatically, along with a 2d graphics program called Cairo.

First, we need to determine if we are talking about permutations or combinantions? In the case of building a solution for a trainset, in which the order of the tracks does matter, we are talking about permutations without repetitions. In that case, the general formula for the number of permutations is the following:

$$n!/(n-r)!$$

Where n is the number of choices, in our case 16 for number of tracks, and r is how many are chosen from the set. For example, the minimilist solution would be a circle, in which 8 pieces are used. So, in order to find the one and only solution of 8 pieces, we would need to check the following number of permutations:

$$16!/(8)! = 518,918,400$$

That is a non-trivial number of permutations to verify that a solution is formed. We would also need to check for solutions that have 9 pieces, 10 pieces, upto 16. So the total number of potential solutions looks like:

$$16!/8! + 16!/7! + 16!/6! + 16!/5! + 16!/4! + 16!/3! + 16!/2! + 16!/1! + 16!/0!$$

It equates to:

$$5.687397556×10^{13}$$

For a more detailed analysis of the problem, see this question on stackexchange.

Most programming languages have functions or libraries for generating permuations, such as for Python. However, using this approach did prove unpractical (runing on my old PC for example) due to the number of solutions that needed to be tested. A solution that worked better was to use a a [K-ary tree or ternary tree][kary-tree] where K=3 and cr=‘curve right’, cl=‘curve left’, and s=‘straight’ and looks like the following:

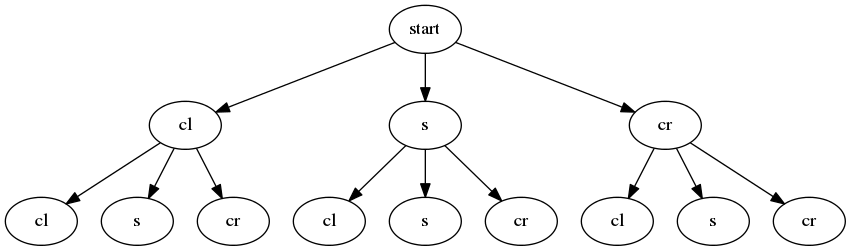
In this approach, I could test the path to a particular node for given depths of tree 8-16. This proved to be more practical as it removes duplicates from the permutations approach. The formula for the total number of nodes in a perfect k-ary tree, with height h is:

$$\left\lfloor\frac{k^{h+1} - 1}{k-1}\right\rfloor$$

In this approach, we want to calculate the total number of nodes with a depth of 16 minus the number of nodes with depth 8, which is the following:

$$\left\lfloor\frac{3^{17} - 1}{2}\right\rfloor - \left\lfloor\frac{3^{7} - 1}{2}\right\rfloor$$

$$=129,140,162.5 - 2186.5 = 129,137,976$$

That is a more managelable number of solutions to calculate. In programatic terms, the algorithm will build a 3-ary (ternary) tree and test the path to a leaf-node at a particular depth. The code for this solution can be found on Github. I use Python generators which will ‘yield’ a path at a depth. It requires no writing/storing paths to disk/memory (space efficient):

def add_children(path, depth):
  if (depth == 1):
    yield path + ['cl']
    yield path + ['s']
    yield path + ['cr']
  else:
    for p in add_children(path + ['cl'], depth - 1): yield p
    for p in add_children(path + ['s'], depth - 1): yield p
    for p in add_children(path + ['cr'], depth - 1): yield p

and where:

def build_tree(depth):
  r = []
  i = 0
  for path in add_children(r, depth):
    i = i+1
    if not valid(path):
      continue
    if duplicate(path):
      continue
    tb = TrackBuilder(str(path))
    if testpath(tb, path):
      solutions.append(path)
      imageid = str(depth) + ‘-’ + str(i)
      tb.createImage(imageid)
      print(str(imageid) + ‘:’ + str(path))
  print(“total checked: “ + str(i))

Once a track path is generated, the following occurs:

• it is tested to see if it is valid (does it have too many straight pieces for example?)
• it is a mirror image? (a circle consisting of 8 cr pieces is the same as 8 cl pieces)
• is it a rotation? (same path but different starting piece)
• it is built using Cairo and tested to see if starting point = ending point and starting arc = ending arc
• if all those conditions pass, an image (png) is generated

Running for depth 8 produced 1 solution, as expected:

$ ./main.py 8
8-1:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’]
total checked: 6561

and the solution looks like:

Running for depth 9 produced 0 solutions:

$ ./main.py 9
total checked: 19683

Running for depth 10 produced 1 solution:

$ ./main.py 10
10-245:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’]
total checked: 59049

and the solution looks like:

Running for depth 11 produced 0 solutions:

$ ./main.py 11
total checked: 177147

Running for depth 12 produced 2 solutions:

$ ./main.py 12
12-1461:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’]
12-2921:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’]
total checked: 531441

and here’s an animated gif showing all solutions for 12 pieces:

Running for depth 13 produced 0 solutions:

$ ./main.py 13
total checked: 1594323

Running for depth 14 produced 9 solutions:

$ ./main.py 14
14-10941:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cr’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cr’]
14-13857:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cr’]
14-15317:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ’s’]
14-15321:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cr’]
14-24069:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cr’]
14-41573:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ’s’]
14-63453:[‘cl’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cl’, ‘cr’]
14-79059:[‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cr’]
14-120341:[‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ’s’]
total checked: 4,782,969

and here’s an animated gif showing all solutions for 14 pieces:

Running for depth 15 produced 0 solutions:

$ ./main.py 15
total checked: 14,348,907

Running for depth 16 produced 15 solutions:

$ ./main.py 16
16-32801:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cr’, ‘cr’, ‘cr’, ‘cr’, ‘cr’, ‘cr’, ’s’, ’s’]
16-91869:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cr’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cr’]
16-100617:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cr’, ‘cl’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cr’]
16-126861:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cr’]
16-144365:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ’s’, ’s’]
16-144377:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cr’, ’s’]
16-144381:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cr’]
16-223113:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cl’, ‘cr’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cr’]
16-239121:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cr’]
16-249357:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cr’]
16-301865:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ’s’, ‘cr’, ‘cl’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ’s’, ’s’]
16-380597:[‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ’s’, ’s’]
16-717393:[‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ‘cr’]
16-721821:[‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cr’]
16-1089293:[‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ’s’, ’s’, ‘cl’, ‘cl’, ‘cl’, ‘cr’, ‘cl’, ‘cl’, ’s’, ’s’]
$ total checked: 43,046,721

and here’s an animated gif showing all solutions for 16 pieces:

A few notes:

• only 1 solution includes a path under the bridge (16-32801).
  
• total solutions = 1(@8) + 0(@9) + 1(@10) + 0(@11) + 4(@12) + 0(@13) + 9(@14) + 0(@15) + 15(@16) = 30 solutions
• personal favorite (16-717393)

There are a few things that could be done for this project:

• It’s not a concurrent solution (only 1 CPU process runs at a time). Calculating solutions for depths of 8-12 ran in under a minute or two … a depth of 16 took an hour (old PC).
• This program finds ‘perfect’ solutions where start point = end point. There is a lot of ‘give’ in the tracks. Several workable solutions exist by bending the tracks to ‘fit’.
  

Thanks for reading. Send me a pull request on Github if you think you have a contribution.

[kary-tree]: https://en.wikipedia.org/wiki/K-ary_tree